Sistem Persamaan Linear

Persamaan linier sama halnya dengan persamaan aljabar , yaitu merupakan sebuah sisitem hitung dalam ilmu matematika dan dapat digambarkan dalam bentuk garis lurus dalam sebuah grafik . Sistem persamaan linier disebut juga dengan sisistem persamaan garis . 

Lalu bagaimanakah cara atau metode dalam menyelesaikan sistem persamaan linier ? Pada pembahasan kali ini , kita akan mempelajari apa itu persamaan linier dan bagaimana metode dalam meyelesaikan persamaan linier secara lengkap dan tepat .

Sistem Persamaan Linear

Sebelum kita mempelajari bagaimana metode dalam menyelesaikan siste persamaan linier , maka kita harus memahami terlebih dahulu mengenai definisi kalimat terbuka dan definisi persamaan serta tentang sistem persamaan linier . Sehingga dalam menyelesaikan persamaan linier kita tidak bingung.

A. Pengertian Kalimat terbuka , persamaan dan persamaan linier 

Kalimat Terbuka , yaitu suatu kalimat yang memiliki atau memuat variabel .

Persamaan , yaitu kalimat terbuka yang menyatakan hubugan sama dengan ( = ) .

Persamaan Linier , yaitu suatu persamaan yang setiap sukunya mengandung konstanta dengan variabelnya berderajat satu ( tunggal ) dan persamaan ini , dapat digambarkan dalam sebuah grafik dalam sistem koordinat kartesius .

Suatu Persamaan akan tetap bernilai benar atau EKWIVALENT ( < = > ) , Apabila ruas kiri dan ruas kanan ditambah atau dikurangi dengan bilangan yang sama .

Bentuk umum persamaan linier :

y = mx + b  

Contoh bentuk persamaan linier :

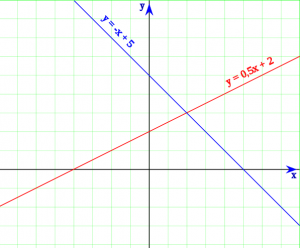
y = -x + 5

y = -05x + 2

Contoh bentuk grafik persamaan linier :

Dari gambar di atas , dapat kita simpulkan bahwasannya m atau gradiennya = 0,5 dan b atau titik potong sumbu y = 2  ( pada garis merah )

B. Metode Penyelesaian Persamaan Linier 

Ada beberapa metode yang dapat digunakan dalam menyelesaikan sebuah permasalahan persamaan linier , metode – metode tersebut adalah :

a. Metode Substitusi

b. Metode Eliminasi

c. Metode Campuran ( eliminasi dan substitusi )

d. Metode grafik

Berikut adalah penjelasan lebih rinci mengenai metode penyelesaian persamaan linier

1. Metode Substitusi 

Metode subsitusi yaitu metode atau cara menyelesaikan persamaan linier dengan mengganti salah satu peubah dari suatu persamaan dengan peubah yang diperoleh dari persamaan linier yang lainnya .

Untuk lebih jelasnya lagi , perhatikan contoh berikut ini :

Diketahui persamaan  x + 3y = 7 dan 2x + 2y = 6 , tentukan Himpunana Penyelesaiannya :

Penyelesaiannya :

x + 3y = 7

< = > x = -3y + 7   . . . .( 1 )

Lalu , masukkan persamaan ( 1 ) ke dalam persamaan ( 2 ) untuk mencari nilai y

2x + 2y = 6

< = > 2 ( -3y + 7 ) + 2y = 6

< = > -6y + 14 + 2y = 6

< = > -6y + 2y = 6 – 14

< = > -4y = – 8

< = > y = 2

Gunakan persamaan antara persamaan ( 1 ) atau ( 2 ) untuk mencari nilai x

x + 3y = 7

< = > x + 3 ( 2 ) = 7

< = > x + 6 = 7

< = > x = 1

Jadi , HP = { 1 , 2 }

2. Metode Eliminasi 

Metode Eliminasi , yaitu metode penyelesaian sistem persamaan linir dengan cara mengeliminasi atau menghilangkan salah satu peubah dengan menambahkan atau mengurangkan dengan menyamakan koefisien yang akan dihilangkan tanpa memperhatikan nilai positif atau negatif .

Apabila peubah yang akan dihilangkan bertanda sama , maka untuk mengeliminasi menggunakan sistem operasi pengurangan . Dan sebaliknya apabila peubah yang akan dihilangkan bertanda berbeda , maka untuk mengaliminasi menggunakan operasi penjumlahan .

Utuk lebih jelasnya , perhatikan contoh berikut ini :

Masih dengan contoh yang sama , namun dengan cara yang berbeda yaitu :

Diketahui dua persamaan  x + 3y = 7 dan 2x + 2y = 6 , tentukan HP dari persamaan tersebut !

Langkah pertama adalah lakukan eliminasi dengan mengurangkan untuk menghilangkan peubah atau koefisien x untuk mengetahui nilai y

2x + 2y = 6   : 2

< = > x + y = 3

lalu , lakukan

x + 3y = 7

x + y = 3   _

2y = 4

y = 2

Langkah selanjutnya adalah lakukan eliminasi dengan mengurangkan untuk menghilangkan peubah atau koefisien y untuk mengetahui nilai x

2x + 2y = 6 | x3 | < = >  6x + 6y = 18

x + 3y = 7 | x 2 | < = >  2x + 6 y = 14      _

                                           4x + 0 = 4

                                               x = 1

Jadi , Himpunan penyelesaian yang dihasilkan sama yaitu HP = { 1 , 2 }

3. Metode Campuran ( antara eliminasi dan substitusi ) 

Yang dimaksud dari metode ini , yaitu kita dalam mencari himpunan penyelesaian menggunakan dua metode boleh gunakan eliminasi terlebih dahulu setelah diketahui salah satu nilai peubah baik itu x atau y maka selanjutnya masukkan ke dalam metode substitusi atau sebaliknya .

Untuk lebih jelasnya , perhatikan contoh berikut :

Diketahui dua persamaan  x + 3y = 7 dan 2x + 2y = 6 , tentukan HP dari persamaan tersebut !

Langkah pertama lakukan metode eliminasi , untuk mecari nilai x

2x + 2y = 6 | x3 | < = >  6x + 6y = 18

x + 3y = 7 | x 2 | < = >  2x + 6 y = 14      _

                                           4x + 0 = 4

                                               x = 1

Selanjutnya substitusikan nilai x ke dalam salah satu persamaan :

x + 3y = 7

< = > 1 + 3y = 7

< = > 3y = 7  – 1

< = > 3y = 6

< = > y = 2

 Maka hasilnyapun sama yaitu HP = { 1 , 2 }

4. Metode Grafik 

Metode grafik , yaitu dengan menggambarkan dua persamaan pada grafik kartesius , dan himpunan penyelesaiannya dihasilkan dari titik potong dari kedua garis tersebut . Yang perlu diperhatikan yaitu ketika menggambar titik sumbu kartesiusnya harus sama dan konsisten .

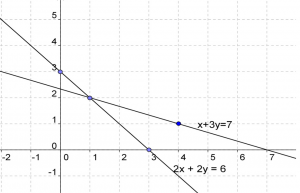
Untuk lebih jelasnya perhatikan gambar grafik berikut :

Gambarlah grafik persamaan x + 3y = 7 dan 2x + 2y = 6 , dan tentukan titik potongnya

Dari gambar di atas , maka kita dapat melihat bahwa titik potongnya berada pada titik { 1 , 2 } dan dengan kata lain HP = { 1 , 2 }

Demikian penjelasan mengenai sistem persamaan linear. Semoga dengan penjelasan diatas kita dapat mengerti apa itu sistem persamaan dan cara – cara dalam menyelesaikannya